Analysis 4: Difference between revisions
No edit summary |
No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[2013 | Back to 2013 Main Page]] | |||
[[2012 | Back to 2012 Main Page]] | |||
In this tutorial you will work through an example linear fit. The example is the trajectory experiment described in the previous tutorials. In this model we had altitude data <math>d_i</math> taken at times <math>t_i</math> that was modeled with a quadratic formula: | In this tutorial you will work through an example linear fit. The example is the trajectory experiment described in the previous tutorials. In this model we had altitude data <math>d_i</math> taken at times <math>t_i</math> that was modeled with a quadratic formula: | ||
| Line 37: | Line 42: | ||
</pre> | </pre> | ||
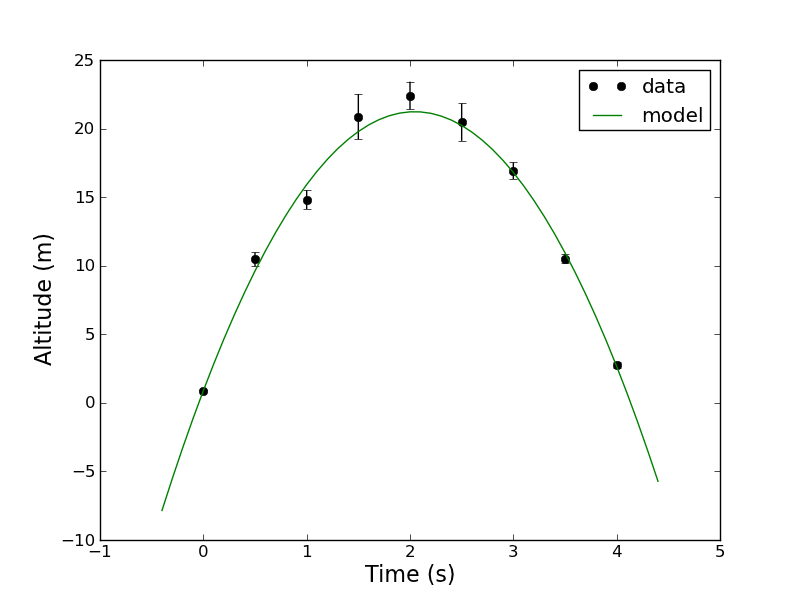
You should also obtain the following graph of the data | You should also obtain the following graph of the data with the model fit | ||
[[File: | [[File:Data_with_model_linear.png]] | ||
Latest revision as of 03:38, 28 January 2013
In this tutorial you will work through an example linear fit. The example is the trajectory experiment described in the previous tutorials. In this model we had altitude data <math>d_i</math> taken at times <math>t_i</math> that was modeled with a quadratic formula:
<math> d_i = a t_i^2 + b t_i + c </math>.
The following example is carried out using the python programming language. A great collection of python tools are downloadable for free (since you are students) here: [1]
Here is a file with the altitude data: media:Altitudes.txt. The first column is time and the following columns altitude data taken at the corresponding time. The multiple columns with repeated data represent repeated experiments (multiple "tosses of the projectile").
Here is the code to analyze this data (change suffix to .py) media:Linear_model.txt. The code is documented with comments (preceded by the "#" character). The code reads in the data, computes the mean and sample variance on the mean of the data at each time. It then computes the best fit, the probability to exceed as well as the variance on the model parameters.
Here is the output that you should get:
time [ 0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. ] mean [ 0.8852 10.455 14.8192 20.8646 22.4106 20.465 16.9212 10.5114 2.7726] std on mean [ 0.04827836 0.50863592 0.68481835 1.64741573 1.01026263 1.36580654 0.60635957 0.34929654 0.22239846] data shape (9,) N_inv shape (9, 9) M shape (9, 3) MT shape (3, 9) a,b,c = [ -4.86139735 19.88867809 0.88890815] var(a,b,c) = 0.0115034026436 0.167905279208 0.00232097475846 [-0.00370815 0.83710214 -1.09698889 1.08081875 1.18992507 0.23813005 0.11883372 -0.43576394 0.11133707] [ 1.37503988e-05 7.00739994e-01 1.20338463e+00 1.16816917e+00 1.41592166e+00 5.67059231e-02 1.41214527e-02 1.89890215e-01 1.23959428e-02] [ 9.32320000e-03 1.03484200e+00 1.87590470e+00 1.08559143e+01 4.08252230e+00 7.46171000e+00 1.47068770e+00 4.88032300e-01 1.97844300e-01] chisq = 8.97399733731 with 6 dof PTE = 0.175045732295
You should also obtain the following graph of the data with the model fit