Analysis 5: Difference between revisions
| Line 38: | Line 38: | ||
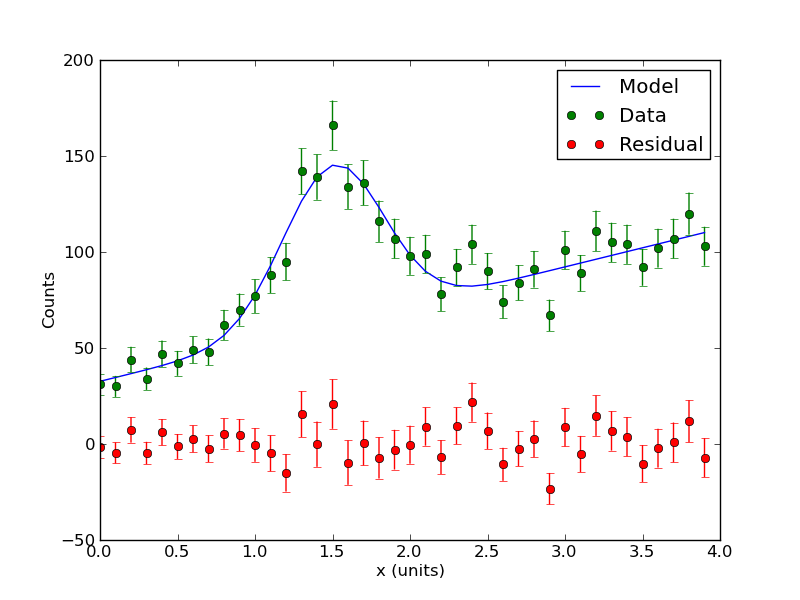
The program should also output some plots. Among them is the best fit model plotted through the data points: | The program should also output some plots. Among them is the best fit model plotted through the data points: | ||
[[ | [[file:Counts_with_fit.png]] | ||
Revision as of 01:14, 11 February 2012
In the past few tutorials, you learned how to fit data using a linear model. While many datasets may be fit with such a model, other datasets, including some that you encounter in the lab course, will not be described by linear models. Remember that a model is linear if it is linear in the parameters, so a nonlinear model must be nonlinear in the parameters. When fitting a nonlinear model, there is generally no analytic solution to the <math>\chi^2</math> minimization problem. Instead, a numerical technique is used to explore parameter space in search of the <math>\chi^2</math> minimum. A standard technique is to start at some point in parameter space and follow the gradient of the function towards the minimum, also using information about the curvature, where useful. A standard algorithm is called the Levenburg-Marquardt algorithm which uses the gradient and Hessian of the <math>\chi^2</math> to find the best fit values and their associated variance. You can learn more about this by reading the associated sections in Press, Teukolsky, Vetterling, Flannery, Numerical Recipes in C (Available online). Also you can check out the associated section in my notes from from last year media: Data_reduction_notes.pdf. Instead of diving into the details here, we provide a worked example.
The following example is carried out using the python programming language. A great collection of python tools are downloadable for free (since you are students) here: [1]
Nonlinear Model Example
Here we introduce some data <math>c_i</math> representing, say, the number of gamma-rays incident on a detector. These data are sorted by their energy <math>e_i</math>. We model the counts as a function of their energy:
<math> c_i = A \exp(-(e_i-B)^2/(2 C^2)) + Dx + E </math>
Here the parameters are the amplitude A, offset B, and width C of a Gaussian peak -- presumably modeling some emission line in the data. There is also a linear background with slope D and offset E. This example is particularly relevant to the nuclear spectroscopy lab. Because this is count data, we can use Poisson statistics to estimate the variance of the data: the variance of <math>c_i</math> is just <math>c_i</math>.
Here is the data for non-linear model and confidence interval example: media:counts.txt. The first column is energy, the second column is counts.
Here is the code (change sufixx to .py): media:Nonlinear_model.txt. The code contains comments so you follow the execution and hopefully reuse it for your own work. The code reads in the data file and fits a the nonlinear model using a Levenburg-Marquardt-based algorithm. The model determines the best fit as well as the parameter covariance matrix (and therefore the errors on the parameters). It also computes the <math>\chi^2</math> value of the best fit and evaluates the probability to exceed this value. The program should print the following values:
[ 0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2. 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3. 3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9] [ 31. 30. 44. 34. 47. 42. 49. 48. 62. 70. 77. 88. 95. 142. 139. 166. 134. 136. 116. 107. 98. 99. 78. 92. 104. 90. 74. 84. 91. 67. 101. 89. 111. 105. 104. 92. 102. 107. 120. 103.] A= 82.7632550246 +/- 6.09661566067 B= 1.50411352295 +/- 0.0243586882858 C= -0.32584820157 +/- 0.0254629737597 D= 19.8662901184 +/- 1.16145499077 E= 32.6492609413 +/- 2.58896966419 Chi-Sq = 36.4655268717 dof = 35 PTE = 0.400407320107
The program should also output some plots. Among them is the best fit model plotted through the data points: